julian apostata hat geschrieben:Ich schreib mal seine Quatschgleichung in einer anderen Form hin.
\cdot\frac{D}{T}) https://de.wikipedia.org/wiki/Algol_(Stern)
https://de.wikipedia.org/wiki/Algol_(Stern)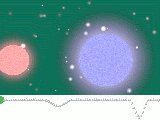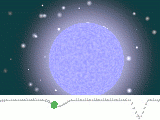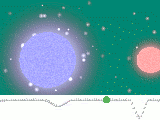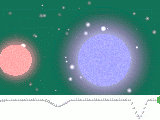
D=93 Jahre T=2.87 Tage ergo D/T=1.1 Mio
0° und 180° das wären die Winkel wo jeweils der eine Partner den anderen bedeckt. Lothar will uns also weismachen, dass man hier eine (Rot)Blauverschiebung von z=6.9 Mio *(v/c) beobachtet.
Grund dv_rg/dα ist hier am größten.
Bei 90° und 270° sollte man laut Lothar keine Verschiebung messen, aber gerade da misst der Astronom z=v/c
Nach der Formel des ungebremsten Delta-Lambda-Effekts
„RG“ = ± V/T*2π*D
ergibt sich für Algol folgendes Bild:
Eine Sonne mit relativ kleiner Größe aber großer Masse wird von einem großen Gasplaneten mit relativ kleiner Masse in T=2,87d=2,48E5 s (auf einer elliptischen Bahn) umlaufen.
Entsprechend dem durchaus möglichen Massenverhältnis beträgt die Umlaufsgeschwindigkeit V der Sonne um den gemeinsamen Schwerpunkt maximal 0,02 m/s.
Dann sollte die Sonne bei ihrer teilweisen Bedeckung durch den Planeten (also bei 0°) in einer Entfernung von D=93a=2,93E9s theoretisch einen Delta-Lambda-Effekt von
„RG“= V/T*2π*D=0,02/2,48E5 *2π*2,93E9 = 1,48E3 m/s=1,48 km/s Blauverschiebung zeigen, bei 90° und 270° einen natürlich unkenntlichen Doppler von 2 cm/s, und bei 180° eine Rotverschiebung von 1,48 km/s.
In der Praxis dürften diese geringen Schwankungen von ±1,48 km/s, sofern sie überhaupt erkennbar sind, aufgrund des Widerspruchs, daß derart geringe Doppelstern-Umlaufsgeschwindigkeiten bei sin i =1 (Bedeckungsbedingung) nicht möglich sind, von den Astronomen als Meßungenauigkeiten interpretiert werden.
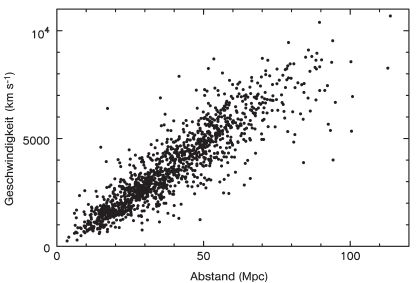
Tatsächlich wird für Algol keine Radialgeschwindigkeitskurve angegeben, obgleich bei einem echten Doppelstern dieser Umlaufszeit und Entfernung eine Doppler-RG-Kurve mit einer Amplitude von etwa 100 km/s deutlich erkennbar sein müßte. Es wird statt dessen für Algol nur eine konstante Radialgeschwindigkeit von 3,7 km/s „Fluchtgeschwindigkeit“ plus/minus 3,9 km/s angegeben, was wiederum zeigt, daß eine Messung der Radialgeschwindigkeit hier möglich ist.
Diese beobachtete Null-Radialgeschwindigkeits-„Kurve“ von Algol ist also kein Widerspruch zum Delta-Lambda-Effekt, sondern sogar wesentlich besser mit dem Delta-Lambda-Effekt und einer Umlaufsgeschwindigkeit < 0,02 m/s zu erklären als nach dem Doppler.
Tatsächlich ist die Null-RG-Kurve von Algol sogar ein Widerspruch zum Doppler, und aus der fehlenden Doppler-RG-Kurve ist zu schließen, daß kein Doppelstern-Umlauf vorliegt, und die beobachteten „Bedeckungen“ keine Bedeckungen sind, sondern (falls die Bedeckung durch den Planeten nicht ausreicht) „Lichtaus“-Effekte als Folge sich verdrehender und entsprechend in andere Richtungen laufender Wellenzüge.
Diese Verdrehung der Wellenzüge in den Bereichen 90° und 270° ist ganz analog herzuleiten wie die Delta-Lambda-Effekt-Stauchung oder -Dehnung der Wellen und Wellenzüge in den Bereichen 0° und 180°, wobei der deutlich begrenzte Verdrehungsbereich und die Größe des Lichtauseffekts dadurch bestimmt sind, daß die ungebremste Verdrehung bzw. Richtungsänderung nur im „Äther“-Mitführungsbereich stattfindet, und danach ebenso gebremst ist wie Wellenlängenänderung. Ein großer Lichtauseffekt wie bei Algol erfordert demnach einen großen Mitführungsbereich infolge großer Masse, was wiederum mit der geringen Umlaufsgeschwindigkeit < 0,02 m/s übereinstimmt.
Insofern widerlegt die fehlende Umlauf-RG-Kurve von Algol die „Doppelstern“- und „Bedeckungs“-Erklärung, und insofern beweist Algol den Delta-Lambda-Effekt und den eine „Bedeckung“ vortäuschenden Verdrehungseffekt. Hierbei stehen die Amplituden der „RG“-Kurve und der „Lichtaus“-Effekt richtig in dem beobachteten zeitlichen Zusammenhang.
Mit freundlichen Grüßen
Lothar Pernes


 ,
, 
 ,
, 
 hat geschrieben:
hat geschrieben: